
Vsebina
- Določite čas v zraku.
- Korak 1
- 2. korak
- 3. korak
- 4. korak
- Določite največjo višino
- Korak 1
- 2. korak
- 3. korak
- Določite prevoženo vodoravno razdaljo.
- Korak 1
- 2. korak
- 3. korak
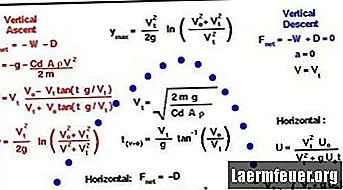
Tu je metoda za izračun poti krogle in natančneje čas v zraku, doseg in najvišja točka njegove poti. V tem primeru so bile nekatere predpostavke poenostavljene pri izračunu: zanemarljiv zračni upor, brez vetra in nezadostna strelna razdalja, da bi lahko Zemljina rotacija začela veljati.
Določite čas v zraku.
Korak 1
Najprej je treba določiti obliko loka. Če je kot sprva navzdol, potem je že znano, da je najvišja točka strelni položaj. Tudi kot navzgor ima lahko cilj najvišjo točko, ne glede na to, ali je ta kot plit ali dovolj visok (h). To lahko določimo v četrtem koraku, ko določimo zračni čas.
2. korak
Če je kot "?" hitrost streljanja je med začetno potjo izstrelka in vodoravno, zato je začetna navpična hitrost V (i) = V.sen?
3. korak
Zračni čas najdemo z enačbo položaja h = V.sen? .T - (0,5) g.t ^ 2, kjer je g = 9,8 metra / sekundo ^ 2. Znane so vse spremenljivke, razen časa v zraku, t, zato je to mogoče rešiti s kvadratno funkcijo: ax ^ 2 + bx + c = 0, zato je x = [-b ± √ (b ^ 2-4ac )] / 2a
4. korak
Če je dovoljeno več kot ena rešitev za t, saj je h> 0, potem prvi rezultat ustreza kdaj je višina = h na poti vzpona, drugi pa kdaj je višina = h na poti spusta. Če je h <0, je bila dovoljena edina resnična rešitev za t, druga pa negativna.
Določite največjo višino
Korak 1
Če je <<0, potem je že znano, da je največja višina začetna višina, h = 0.
2. korak
Če je bil t večkrat, t, v katerem krogla sega h, potem najmanjši t ustreza poti leta, kjer je h najvišja točka. Najvišji t ustreza krogli, ki je dosegla višjo višino, preden se je vrnila na h, da jo rešite z uporabo formule V (t) = V (0) - 9,8t, da poiščete vrednost t, ko je navpična hitrost nič. Z drugimi besedami, za koliko časa je t, V.sen? = 9,8t.?
3. korak
Če rešimo t in povežemo formulo višine, imamo največjo višino: hm = V.sen? - 4,9t ^ 2. Enak pristop se uporablja za rešitev največje višine, če je bila dovoljena samo ena rešitev za t.
Določite prevoženo vodoravno razdaljo.
Korak 1
Za določitev vodoravne razdalje, ki jo je prevozila čas, ko krogla doseže višino h, najprej izračunamo začetno vodoravno hitrost krogle: v (i) = V.cos (?).
2. korak
Nadomestite čas, t, ko krogla doseže končno višino A v položaju formule z uporabo vodoravne hitrosti: A = V.cosΘ.t. Ob predpostavki, da na desni strani ni zračnega upora in ni pospeška.
3. korak
Če je bila višina v h večkrat t, bosta veljali položaji "A", najvišja dosežena točka pa bo hm za manjšo od obeh "A". Zdaj sta znana vodoravni in navpični končni položaj in najvišja dosežena točka, kar določa smer krogle.