Vsebina
Vsi pravokotni trikotniki imajo kot 90 °. Uporabljajo se pri matematiki za posebne izračune, med drugim za iskanje natančne razdalje med dvema točkama. Pomagajo tudi določiti prevelike ali pretežke izračune višin in razdalj. Imajo veliko posebnih lastnosti, ki so osnova trigonometrije.

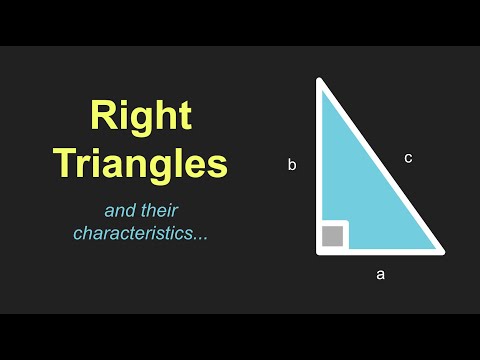
Anatomija pravokotnega trikotnika
Dve manjši strani trikotnika pravimo kot kateti. Običajno se označujejo s črkama "a" in "b". Tretja stran, nasproti kota 90 °, se imenuje hipotenuza in se običajno imenuje črka "c".
Pitagorejska teorema
Pitagorejski izrek določa, da je vsota kvadratov nog enaka kvadratu hipotenuze. Z drugimi besedami, a² + b² = c², kjer sta "a" in "b" kateti, "c" pa hipotenuza. Če poznamo dvostransko merilo pravokotnega trikotnika, bomo uporabili izrek, da bi našli tisto iz tretjega. To se v veliko primerih uporablja za iskanje težko merljivih razdalj ali dolžin. Na primer, če veste, da ste odpeljali 10 blokov proti jugu in nato 6 blokov proti zahodu, od hiše do središča mesta in želite vedeti, kakšna je neposredna razdalja med obema krajema, lahko ugotovite, da 10² + 6² = (direktna razdalja) ², sklepamo, da so približno 12 ravnih blokov.
Trikotniki 45-45-90
Eden od treh pravokotnih trikotnikov je 45-45-90. Oblikuje se z risanjem diagonalne črte od enega vogala do drugega v kvadratu. On je edini, katerega noge merijo natanko enako. Torej je edina vrsta, ki je tudi enakokračni trikotnik. Ime 45-45-90 izhaja iz merila njegovih notranjih kotov. Ima zahtevani kot 90 ° in dva manjša, 45 °. Piščanci in hipotenuza imajo vedno razmerje 1: .2. Za ta trikotnik morate poznati dolžino samo ene strani, da bi našli druge dve. Dolžina hipotenuze je enaka merilu ene noge, deljene z .2.
Trikotniki 30-60-90
Tako kot trikotnik 45-45-90 ima tudi ime 30-60-90 zaradi 30, 60 in 90-stopinjske mere notranjih kotov. Oblikuje se z rezanjem enakostraničnega trikotnika na pol. Njene stranice tvorijo tudi konstantno razmerje 1: :3: 2. Spodnji del noge je neposredno nasproti kota 30 ° in vedno meri polovico dolžine hipotenuze, ki je nasproti kotu 90 °. Večja noga, nasproti kota 60 °, meri dolžino manjših časov ,3 ali polovico hipotenuze .3. Zaradi tega morate poznati samo dolžino ene strani, da najdete dolžino drugih dveh.